

Institute of Formal and Applied Linguistics
Charles University, Czech Republic
Faculty of Mathematics and Physics
NPFL103 – Information Retrieval
"Information retrieval is the task of searching a body of information for objects that statisfied an information need."
This course is offered at the Faculty of Mathematics and Physics to graduate students interested in the area of information retrieval, web search, document classification, and other related areas. It is based on the book Introduction to Information Retrieval by Christopher D. Manning, Prabhakar Raghavan, Hinrich Schütze. The course covers both the foundations of information retrieval and some more advanced topics.
About
SIS code: NPFL103
Semester: winter
E-credits: 5
Examination: 2/2 C+Ex
Lecturer: Pavel Pecina, pecina@ufal.mff.cuni.cz
Language: The course is taught in English. All the materials are in English, the homework assignments and/or exam can be completed in English or Czech.
Timespace Coordinates
- Tuesdays, 10:40-12:10 (12:20-13:50) S9, Malostranské nám. 25
- Consultations upon request.
News
- Assignment 1 deadline: Nov 25, 2024 23:59
- Assignment 2 deadline: Dec 31, 2024 23:59
- Preliminary exam date: Jan 14, 2025.
- The course will start on Oct 8, 2024.
Lectures
1. Introduction, Boolean retrieval, Inverted index, Text preprocessing Slides Questions
2. Dictionaries, Tolerant retrieval, Spelling correction Slides Questions
3. Index construction and index compression Slides Questions
4. Ranked retrieval, Term weighting, Vector space model Slides Questions
5. Ranking, Complete search system, Evaluation, Benchmarks Slides 1. Vector Space Models Questions
6. Result summaries, Relevance Feedback, Query Expansion Slides Questions
7. Probabilistic information retrieval Slides Questions
8. Language models, Text classification Slides 2. Information Retrieval Frameworks Questions
9. Vector space classification Slides Questions
10. Document clustering Slides Questions
11. Latent Semantic Indexing Slides Questions
12. Web search, Crawling, Duplicate detection Slides Questions
Assignments
2. Information Retrieval Frameworks Slides
Prerequisities
No formal prerequisities are required. Students should have a substantial programming experience and be familar with basic algorithms, data structures, and statistical/probabilistic concepts.
Passing Requirements
To pass the course, students need to complete two homework assignments and a written test. See grading for more details.
License
Where stated, the teaching materials for this course are available under CC BY-SA 4.0.
Note: The slides available on this page might get updated during the semestr. For each lecture, any updates will be published before the lecture starts.
1. Introduction, Boolean retrieval, Inverted index, Text preprocessing
- definition of Information Retrieval
- boolean model, boolean queries, boolean search
- inverted index, dictionary, postings, index construction, postings list intersection
- text processing, tokenization, term normalization, diacritics, case folding, stop words, lemmatization, stemming, Porter algorithm
- phrase queries, biword index, positional index, proximity search
2. Dictionaries, Tolerant retrieval, Spelling correction
- dictionary data structures, hashes, trees
- wildcard queries, permuterm index, k-gram index
- spelling correction, correcting documents, correcting queries, spellchecking dictionaries
- edit distance, Levenshtein distance, weighted edit distance, query spelling correction
- Soundex
3. Index construction and index compression
- Reuters RCV1 collection
- sort-based index construction, Blocked sort-based indexing, Single-pass in-memory indexing
- distributed indexing, Map Reduce, dynamic indexing
- index compression, Heap's law, Zipf's law, dictionary compression, postings compression
4. Ranked retrieval, Term weighting, Vector space model
- ranked retrieval vs. boolen retrieval, query-document scoring, Jaccard coefficient
- Bag-of-words model, term-frequency weighing, document-frequency weighting, tf-idf, collection frequency vs. document frequency
- vector space model, measuring similarity, distance vs. angle, cosine similarity
- length normalization, cosine normalization, pivot normalization
5. Ranking, Complete search system, Evaluation, Benchmarks
Nov 12 Slides 1. Vector Space Models Questions
- ranking, motivation and implementation, document-at-a-time vs. term-at-a-time processing
- tiered indexes
- query processing, query parser
- evaluation, precision, recall, F-measure, confusion matrix, precision-recall trade-off, precision-recall curves, average precision, mean everage precision, averaged precision-recall graph, A/B testing
- existing benchmarks
6. Result summaries, Relevance Feedback, Query Expansion
- static summaries, dynamic summaries
- relevance feedback, Rocchio algorithm, pseudo-relevance feedback
- query expansion, thesaurus construction
7. Probabilistic information retrieval
- probabilistic approaches to IR
- Probabilistic Ranking Principle
- Binary Independence Models
- Okapi BM25
8. Language models, Text classification
Dec 3 Slides 2. Information Retrieval Frameworks Questions
- language models for IR
- smoothing (Jelinek-Mercer, Dirichlet, Add-one)
- text classification
- Naive Bayes classifier
- evaluation of text classification, micro averaging, macro averaging,
9. Vector space classification
- vector space classification
- k Nearest Neighbors
- linear classifiers
- Support Vector Machines
10. Document clustering
- document clustering in IR
- vector space clustering
- K-means clustering
- setting number of clusters
- evaluation of clustering
- hierarchical clustering, dendrogram, cluster similarity measures
11. Latent Semantic Indexing
- Singular Value Decomposition
- dimensionality reduction
- LSI in information retrieval
- LSI as soft clustering
12. Web search, Crawling, Duplicate detection
- Web search, Web information Retrieval
- Structure of the Web
- Query types
- Web crawling, robots.txt
- Duplicate detection, Sketches
- Spam detection
Lecture 1 Questions
Key concepts
Information retrieval, Information need, Query, Document relevance; Boolean model, Boolean query; Word, Term, Token; Text normalization, Stemming, Lemmatization; Stopwords, Stopword removal; Inverted index, Dictionary, Postings, Postings intersection; Biword index, Positonal index; Phrasal search, Proximity search.
Exercise 1.1
Draw the postings for terms rise and home that would be built for the following document collection:
| Doc1: | new home sales top forecasts |
| Doc2: | home sales rise in july |
| Doc3: | increase in home sales in july |
| Doc4: | july new home sales rise |
Exercise 1.2
Query optimization is the process of selecting how to organize the work of answering a query so that the least total amount of work needs to be done by the system. Recommend a query processing order for the following two queries:
trees AND skies AND kaleidoscope(tangerine OR trees) AND (marmalade OR skies) AND (kaleidoscope OR eyes)
and the postings list sizes:
| Term | Postings Size |
|---|---|
| eyes | 213,312 |
| kaleidoscope | 87,009 |
| marmalade | 107,913 |
| skies | 271,658 |
| tangerine | 46,653 |
| trees | 316,812 |
Exercise 1.3
For a conjunctive query, is processing postings lists in order of size guaranteed to be optimal?
Explain why it is, or give an example where it isn’t.
Exercise 1.4
Write out a postings merge algorithm for the query:
x OR y
Exercise 1.5
How should the following Boolean query be handled?
x AND NOT y
Why is naive evaluation of this query normally very expensive?
Write out a postings merge algorithm that evaluates this query efficiently.
Exercise 1.6
Are the following statements true or false?
- In a Boolean retrieval system, stemming never lowers precision.
- In a Boolean retrieval system, stemming never lowers recall.
- Stemming increases the size of the vocabulary.
- Stemming should be invoked at indexing time but not while processing a query.
Exercise 1.7
The following pairs of words are stemmed to the same form by the Porter stemmer. Which pairs would you argue shouldn’t be conflated. Give your reasoning.
- abandon/abandonment
- absorbency/absorbent
- marketing/markets
- university/universe
- volume/volumes
Lecture 2 Questions
Key concepts
Implementation of dictionary and postings in inverted index, B-trees; Wildcard queries, Permuterm index, k-gram index; Spelling correction (isolated, context-sensitive), Spelling correction in IR, (Weighted) Edit distance, Levenshtein distance, Soundex.
Exercise 2.1
Assume a biword index. Give an example of a document which will be returned
for a query of New York University but is actually a false positive which should not be
returned.
Exercise 2.2
How could an IR system combine use of a positional index and use of stop words? What is the potential problem, and how could it be handled?
Exercise 2.3
In the permuterm index, each permuterm vocabulary term points to the original vocabulary term(s) from which it was derived. How many original vocabulary terms can there be in the postings list of a permuterm vocabulary term?
Exercise 2.4
Write down the entries in the permuterm index dictionary that are generated by the term mama.
Exercise 2.5
If you wanted to search for s*ng in a permuterm wildcard index, what key(s) would one do the lookup on?
Exercise 2.6
Vocabulary terms in the postings of in a k-gram index are lexicographically ordered. Why is this ordering useful?
Exercise 2.7
If |a| denotes the length of string a, show that the edit distance between a and b is never more than max{|a|, |b|}.
Exercise 2.8
Compute the edit distance between paris and alice. Write down the 5 × 5 array of distances between all prefixes as computed by the Levenshtein algorithm.
Exercise 2.9
Consider the four-term query catched in the rye and suppose that each of the query terms has five alternative terms suggested by isolated-term correction. How many possible corrected phrases must we consider if we do not trim the space of corrected phrases, but instead try all six variants for each of the terms?
Lecture 3 Questions
Key concepts
Index construction (sort-based, blocked sort-based, single-pass); Distributed indexing, MapReduce; Dynamic indexing, Logarithmic index merging; Index compression, lossy vs. loss-less, Heap's law, Zipf's law; Dictionary compression (as a string, with blocking, with front coding); Postings compression (gap encoding).
Exercise 3.1
For n = 2 and 1 ≤ T ≤ 30, perform a step-by-step simulation of the Logarithmic merge algorithm. Create a table that shows, for each point in time at which T = 2 ∗ k tokens have been processed (1 ≤ k ≤ 15), which of the three indexes l0, . . . , l3 are in use. The first three lines of the table are given below.
| I 3 | I 2 | I 1 | I 0 | |
|---|---|---|---|---|
| 2 | 0 | 0 | 0 | 0 |
| 4 | 0 | 0 | 0 | 1 |
| 6 | 0 | 0 | 1 | 0 |
| 8 | ? | ? | ? | ? |
Exercise 3.2
An auxiliary index can impair the quality of collection statistics. An example is the term weighting method idf, which is defined as log(N/dfi) where N is the total number of documents and dfi is the number of documents that term i occurs in. Show that even a small auxiliary index can cause significant error in idf when it is computed on the main index only. Consider a rare term that suddenly occurs frequently (e.g., Flossie as in Tropical Storm Flossie).
Exercise 3.3
Assuming one machine word per posting, what is the size of the uncompressed (nonpositional) index for different tokenizations based on Slide 48? How do these numbers compare with numbers on Slide 71?
Exercise 3.4
Estimate the space usage of the Reuters-RCV1 dictionary with blocks of size k = 8 and k = 16 in blocked dictionary storage.
Lecture 4 Questions
Key concepts
Boolean rerieval vs. Ranked retrieval, document-query scoring; Bag-of-Words model; Term weighting, Term frequency, Document frequency, TF-IDF; Vector space model, Similarity in vector space, Length normalization, Pivoted length normalization.
Exercise 4.1
What is the idf of a term that occurs in every document? Compare this with the use of stop word lists.
Exercise 4.2
Consider the table of term frequencies for 3 documents denoted Doc1, Doc2, Doc3 (bellow) and compute the tf-idf weights for the terms car, auto, insurance, best, for each document, using the idf values in the following table:
| term | df | idf |
|---|---|---|
| car | 18,165 | 1.65 |
| auto | 6,723 | 2.08 |
| insurance | 19,241 | 1.62 |
| best | 25,235 | 1.5 |
| Doc1 | Doc2 | Doc3 | |
|---|---|---|---|
| car | 27 | 4 | 24 |
| auto | 3 | 33 | 0 |
| insurance | 0 | 33 | 29 |
| best | 14 | 0 | 17 |
Exercise 4.3
Can the tf-idf weight of a term in a document exceed 1?
Exercise 4.4
How does the base of the logarithm in idf affect the calculation of the tf-idf score for a given query and a given document? How does the base of the logarithm affect the relative scores of two documents on a given query?
Exercise 4.5
If we were to stem jealous and jealousy to a common stem before setting up the vector space, detail how the definitions of tf and idf should be modified.
Exercise 4.6
Recall the tf-idf weights computed in Exercise 4.2. Compute the Euclidean normalized document vectors for each of the documents, where each vector has four components, one for each of the four terms.
Exercise 4.7
Verify that the sum of the squares of the components of each of the document vectors in Exercise 4.6 is 1 (to within rounding error). Why is this the case?
Exercise 4.8
With term weights as computed in Exercise 4.6, rank the three documents by computed score for the query car insurance, for each of the following cases of term weighting in the query:
- The weight of a term is 1 if present in the query, 0 otherwise.
- Euclidean normalized *idf*.
Exercise 4.9
Show that if a query vector and document vectors are all normalized to unit vectors, then the rank ordering produced by Euclidean distance is identical to that produced by cosine similarities.
Exercise 4.10
In turning a query into a unit vector we can assigned equal weights to each of the query terms. What other principled approaches are plausible?
Lecture 5 Questions
Key concepts
Importance of ranking in IR; Computing top-k results, Composite scores (PageRank), Document-at-a-time processing, Term-at-a-time processing; Tiered indexes; Evaluation, Document relevance, Confusion matrix, Precision, Recall, F-measure, Precision-recall trade-off, Precision-recall curve, Averaged precision, A/B testing, Benchmarking, test collections.
Exercise 5.1
An IR system returns 8 relevant documents, and 10 nonrelevant documents. There are a total of 20 relevant documents in the collection. What is the precision of the system on this search, and what is its recall?
Exercise 5.2
Derive the equivalence between the two formulas for F measure on slide 51 (using α ad β as parameters), given that α = 1/(β2 + 1).
Exercise 5.3
Must there always be a break-even point between precision and recall? Either show there must be or give a counter-example.
Exercise 5.4
What is the relationship between the value of F1 and the break-even point?
Exercise 5.5
The following list of Rs and Ns represents relevant (R) and nonrelevant (N) returned documents in a ranked list of 20 documents retrieved in response to a query from a collection of 10,000 documents. The top of the ranked list (the document the system thinks is most likely to be relevant) is on the left of the list. This list shows 6 relevant documents. Assume that there are 8 relevant documents in total in the collection.
R R N N N N N N R N R N N N R N N N N R
- What is the precision of the system on the top 20?
- What is the F1 on the top 20?
- What is the uninterpolated precision of the system at 25% recall?
- What is the interpolated precision at 33% recall?
- Assume that these 20 documents are the complete result set of the system. What is the MAP for the query?
Lecture 6 Questions
Key concepts
Presenting IR results, Summaries, Snippets; Relevance feedback, Rocchio algorithm, Positive vs. negative feedback, Pseudo-relevance feedback; Query expansion, thesaurus-based, co-occurence-based.
Exercise 6.1
In Rocchio’s 1971 algorithm (SMART), what weight setting for α/β/γ does a “Find pages like this one” search correspond to?
Exercise 6.2
Give three reasons why relevance feedback has been little used in web search.
Exercise 6.3
Why is positive feedback likely to be more useful than negative feedback to an IR system? Why might only using one nonrelevant document be more effective than using several?
Lecture 7 Questions
Key concepts
Probability Ranking Principle, Binary Independece Model (assumptions), Retrieval Status Value, BM25 extension.
Exercise 7.1
What are the differences between standard vector space tf-idf weighting and the BIM probabilistic retrieval model (in the case where no document relevance information is available)?
Exercise 7.2
Let Xt be a random variable indicating whether the term t appears in a document. Suppose we have |R| relevant documents in the document collection and that Xt = 1 in s of the documents. Take the observed data to be just these observations of Xt for each document in R. Show that the MLE for the parameter pt = P(Xt = 1|R = 1,q), that is, the value for pt which maximizes the probability of the observed data, is pt = s/|R|.
Lecture 8 Questions
Key concepts
Language models for IR (principles, parameter estimation, smoothing, Jelinek-Mercer, Dirichlet); Text classification, Naive Bayes classification (classification rule, parameter estimation, smoothing, assumptions); Evaluation of classification (Precision, Recall, F), One-class vs. Multi-class classification (Micro, Macro).
Exercise 8.1
Including STOP probabilities in the calculation, what will the sum of the probability estimates of all strings in the language of length 1 be? Assume that you generate a word and then decide whether to stop or not (i.e., the null string is not part of the language).
Exercise 8.2
How might a language model be used in a spelling correction system? In particular, consider the case of context-sensitive spelling correction, and correcting incorrect usages of words, such as their in Are you their?
Exercise 8.3
Consider making a language model from the following training text:
the martian has landed on the latin pop sensation ricky martin
- Under a MLE-estimated unigram probability model, what are P(the) and P(martian)?
- Under a MLE-estimated bigram model, what are P(sensation|pop) and P(pop|the)?
Exercise 8.4
Suppose we have a collection that consists of the 4 documents given in the below table.
| DocID | Document text |
|---|---|
| Doc1 | click go the shears boys click click click |
| Doc2 | click click |
| Doc3 | metal here |
| Doc4 | metal shears click here |
Build a query likelihood language model for this document collection. Assume a mixture model between the documents and the collection, with both weighted at 0.5. Maximum likelihood estimation (MLE) is used to estimate both as unigram models. Work out the model probabilities of the queries click, shears, and hence click shears for each document, and use those probabilities to rank the documents returned by each query. Fill in these probabilities in the below table:
| Query | Doc1 | Doc2 | Doc3 | Doc4 |
|---|---|---|---|---|
| click | ||||
| shears | ||||
| click shears |
What is the final ranking of the documents for the query click shears?
Exercise 8.5
The rationale for the positional independence assumption is that there is no useful information in the fact that a term occurs in position k of a document. Find exceptions. Consider formulaic documents with a fixed document structure.
Lecture 9 Questions
Key concepts
Vector space classification, k-nn classification (principle, complexity, probabilistic variant); Linear vs. non-linear classfiers; Multi-class classification (one-of, any-of); Support Vector Machines (large margin classification, separability, Slack variables).
Exercise 9.1
Prove that the number of linear separators of two classes is either infinite or zero.
Exercise 9.2
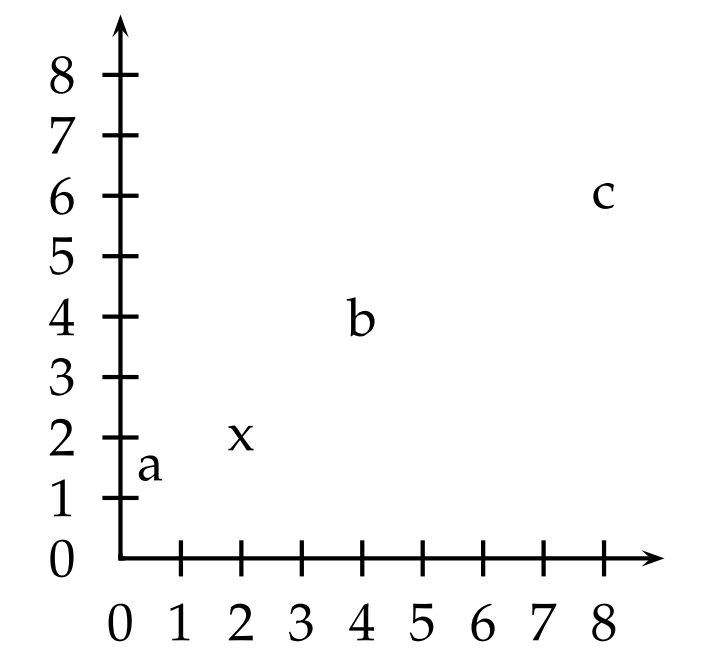
Which of the three vectors a = (0.5, 1.5), x = (2, 2), b = (4, 4), and c = (8, 6) is:
- most similar to x according to dot product similarity
- most similar to x according to cosine similarity
- closest to x according to Euclidean distance?
Exercise 9.3
What is the minimum number of support vectors that there can be for a data set (which contains instances of each class)?
Lecture 10 Questions
Key concepts
Clustering (comparison with classificaton, cluster hypothesis); Clustering in IR; Flat vs. Hierarchical clustering; Hard vs. Soft clustering; K-means clustering (algorithm, convergence vs. optimality, RSS); Evaluation of clustering (Purity, Rand index); Optimization of number of clusters; Hierarchical clustering (aglomerative, bi-secting), cluster similarity, problems (chaining, inversions).
Exercise 10.1
Define two documents as similar if they have at least two proper names like Clinton or Sarkozy in common. Give an example of an information need and two documents, for which the cluster hypothesis does not hold for this notion of similarity.
Exercise 10.2
Make up a simple one-dimensional example (i.e. points on a line) with two clusters where the inexactness of cluster-based retrieval shows up. In your example, retrieving clusters close to the query should do worse than direct nearest neighbor search.
Exercise 10.3
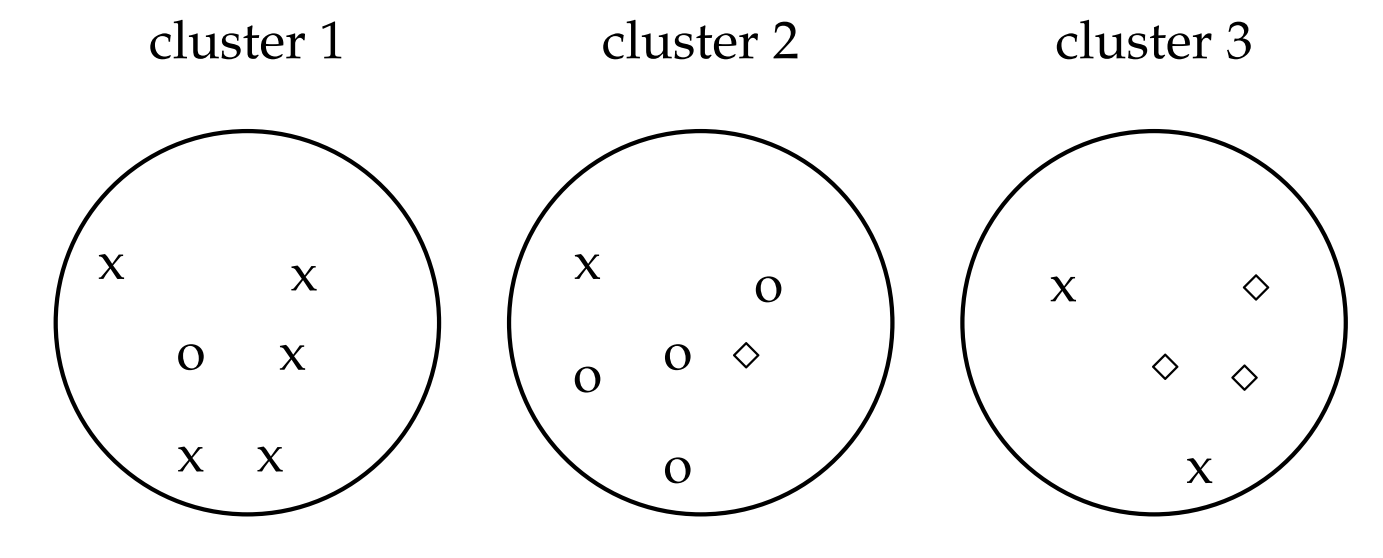
Purity as an external evaluation criterion for cluster quality. Majority class and number of members of the majority class for the three clusters are: x, 5 (cluster 1); o, 4 (cluster 2); and ⋄, 3 (cluster 3). Purity is (1/17) × (5 + 4 + 3) ≈ 0.71.
Replace every point d with two identical copies of d in the same class in the above figure.
- Is it less difficult, equally difficult or more difficult to cluster this set of 34 points as opposed to the 17 points in the figure
- Compute purity and RI for the clustering with 34 points. Which measures increase and which stay the same after doubling the number of points?
- Given your assessment in (i) and the results in (ii), which measures are best suited to compare the quality of the two clusterings?
Exercise 10.4
Why are documents that do not use the same term for the concept car likely to end up in the same cluster in K-means clustering?
Exercise 10.5
Two of the possible termination conditions for K-means were (1) assignment does not change, (2) centroids do not change. Do these two conditions imply each other?
Exercise 10.6
For a fixed set of N documents there are up to N2 distinct similarities between clusters in single-link and complete-link clustering. How many distinct cluster similarities are there in GAAC and centroid clustering?
Exercise 10.7
Consider running 2-means clustering on a collection with documents from two different languages. What result would you expect? Would you expect the same result when running an HAC algorithm?
Lecture 11 Questions
Key concepts
Latent Semantic Indexing (principle, SVD, dimensionality reduction); LSI in IR; LSI as soft clustering;
Lecture 12 Questions
Key concepts
Web crawling (principles, sub-tasks, robots.txt), Mercator URL frontier (principles); Duplicate detection, Near duplicate detection (shingles, sketches).
Exercise 12.1
Why is it better to partition hosts (rather than individual URLs) between the nodes of a distributed crawl system?
Exercise 12.2
Why should the host splitter precede the Duplicate URL Eliminator?
1. Vector Space Models
Deadline: Dec 1, 2024 23:59 Slides 100 points
- Develop an experimental retrieval system based on inverted index and vector space model.
- Experiment with methods for text processing, query construction, term and document weighting, length normalization, similarity measurement, etc.
- Optimize the system on provided test collections (in English and Czech).
- Write a detailed report on your experiments.
- Submit the results for the training and test queries.
- Prepare a presentation and present your results during the course practicals.
- Detailed instructions (with a link to data download) will be distributed via email to all registered students.
2. Information Retrieval Frameworks
Deadline: Dec 29, 2024 23:59 Slides 100 points
- Learn about publicly available information retrieval frameworks and choose one of them (no restrictions)
- Use the selected framework to setup/implement an IR system.
- Optimize the system on the provided test collections (the same as in Assignment 1)
- Write a detailed report on your experiments.
- Submit the results for the training and test queries.
- Present your results during the course practicals.
- Detailed instructions will be distributed via email to all registered students.
Homework assignments
- There are two homework assignments during the semester with a fixed deadline announced on the webpage.
- The assignments are to be worked on independently and require a substantial amount of programming, experimentation, and reporting to complete.
- Students will present their solutions during the practicals in 5-10 minute presentations.
- The assignments will be awarded by 0-100 points each.
- Late submissions received up to 2 weeks after the deadline will be penalized by 50% point reduction.
- Submissions received later than 2 weeks after the deadline will be awarded 0 points.
Exam
- The exam in a form of a written test takes places at the end of semester (up to three terms).
- The test includes approximately 20 questions covered by the topics discussed during the lectures, similar to the ones in questions
- The maximum duration of the test is 90 minutes.
- The test will be graded by 0-100 points.
Final Grading
- Completion of both the homework assignments and exam is required to pass the course.
- The students need to earn at least 50 points for each assignment (before any late submission penalization) and at least 50 points for the test.
- The points received for the assignments and the test will be available in the Study group roster in SIS.
- The final grade will be based on the average results of the exam and the two homework assignments, all three weighted equally:
- ≥ 90%: grade 1 (excellent)
- ≥ 70%: grade 2 (very good)
- ≥ 50%: grade 3 (good)
- < 50%: grade 4 (fail)
Plagiarism
- No plagiarism will be tolerated.
- All cases of plagiarism will be reported to the Student Office.

Introduction to Information Retrieval
Christopher D. Manning, Prabhakar Raghavan, Hinrich Schütze Cambridge University Press, 2008, ISBN: 978-0521865715.
Available online.

Information Retrieval, Algorithms and Heuristics
David A. Grossman and Ophir Frieder, Springer, 2004, ISBN 978-1402030048.

Modern Information Retrieval
Ricardo Baeza-Yates and Berthier Ribeiro-Neto, Addison Wesley, 1999, ISBN: 978-0201398298.

