Content
Node types
In this text we present the main principles of the tectogrammatical representation applied to English and use English examples, but features that are not language-specific to English apply to the Czech tectogrammatical representation as well.
The tectogrammatical representation uses eight types of nodes. They differ in their function as well as in their inner structure (attribute values). The node type is one of the attributes of the inner node structure (nodetype). They are:
Figureá1
- complex nodes
- atomic nodes
- quasi-complex nodes
- paratactic structure root nodes
- phraseme nodes
- foreign-language nodes
- list structure root nodes
- the technical root node
Complex nodes
Complex nodes represent most regular words occurring in the text, except the negation particle, conjunctions and punctuation as roots of paratactic constructions and expressions such as probably, fortunately and however, which belong to what Quirk et al. call disjuncts and (in a few cases) conjuncts. Complex nodes are calles 'complex', since they have the most complex inner structure. They represent mostly autosemantic words with their numerous grammatical categories. These categories are represented by grammatemes (e.g. "number", "tense" and "semantic part of speech"). Nodes of other types do not contain grammatemes. Complex nodes are defined by nodetype=complex.
Figureá2
Atomic nodes
Atomic nodes represent the negation particle (t-lemma #Neg) and expressions such as probably, fortunately and however, which belong to what Quirk et al. call disjuncts and (in a few cases) conjuncts. The atomic nodes are typically labeled by the functors ATT, CM, MOD, PREC, PARTL or RHEM and are defined as nodetype=atom.
Quasi-complex nodes
These are nodes that represent generated nodes (is_generated="1") with t-lemma substitutes (e.g. #Cor). Hence we can say that quasi-complex nodes (nodetype=qcomplex) always have a t-lemma substitute. On the other hand, not all nodes with t-lemma substitutes must be quasi-complex nodes, as we are going to see soon.
Figureá3
Paratactic structure root nodes
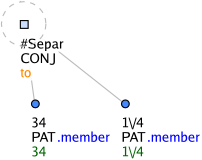
Paratactic structure root nodes are defined as nodetype=coap. These are nodes that represent coordinating conjunctions (and sometimes punctuation - e.g. the comma in the apposition Martin, my best friend. Each punctuation is represented by its specific t-lemma substitute (e.g. #Comma, #Bracket). All paratactic structure root nodes represent real tokens occurring in the text, with one exception: the generated node with the t-lemma substitute #Separ. That is inserted whenever a structure is perceived as a paratactic structure but it lacks a natural paratactic structure root node. It is quite rare. Typically we insert #Separ in composite numbers (Figureá1).
Phraseme nodes
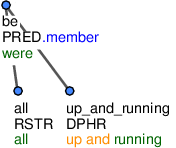
Phrasemes usually consist of more than one word. Longer parts of phrasemes are not structurally analyzed any longer, but they are collapsed into one common node with the functor DPHR (Figureá2). All nodes with this functor have nodetype=dphr.
Foreign-language nodes
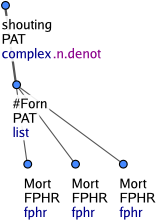
These nodes represent foreign-language expressions. They get the functor FPHR and their nodetype is also nodetype="fphr". See Figureá3.
Figureá4
List structure root nodes
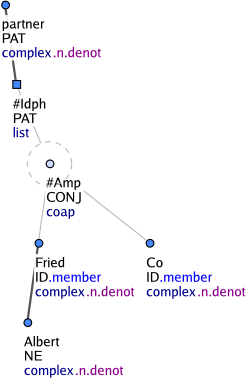
Figureá5
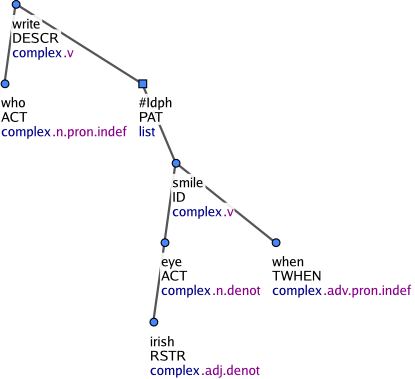
Unlike phrasemes, foreign expressions consisting of several tokens are not collapsed into one single t-node. Nevertheless, their syntactic structure is not analyzed. Each word of the foreign-language sequence gets its own t-node and these nodes become sisters. The entire sequence is governed by a generated node with the t-lemma substitute #Forn. This node has the nodetype nodetype="list". Nodes of this type govern list structures and have either the t-lemma #Forn or #Idph. Figureá3 shows a multi-word foreign expression. While the nodes with the t-lemma #Forn govern foreign-language expressions, the nodes with the t-lemma #Idph always govern proper names ("identification structures") which are not governed by a generic descriptor (e.g. novel, song) and which are constituted by a paratactic phrase, a prepositional group, an adjective or adverb, or by a verb clause (Figureá4 and Figureá5). The effective children of such a structure (i.e. when the coap nodes are ignored) get the functor ID. Modifiers of foreign-language expressions as well as of identification structures are also governed by the list-structure nodes with the t-lemmas #Forn and #Idph (Figureá6).
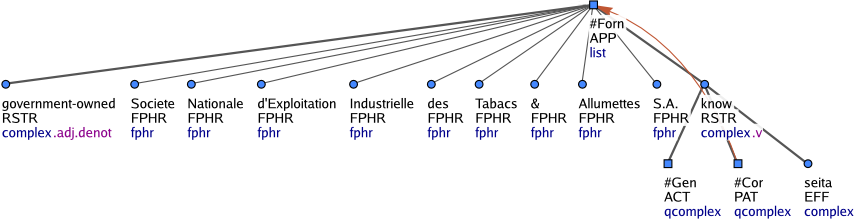
Figureá6
The technical root node
Each tree has one technical root node, which has nodetype="root". It stores the ID of the given tree. Like on the analytical layer, the tree ID encodes the language, the corpus, the layer and the number of the given sentence. It also has the attribute ord ("order"), whose value is always 0.






