Monte Carlo
Jak s využitím generátoru náhodných čísel spočítat konstantu π?
Postup:
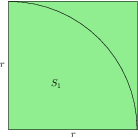
Generujeme opakovaně náhodné souřadnice ve čtverci rxr (viz. obrázek). Pokaždé zkontrolujeme, jestli jsme se trefili dovnitř čtvrtkružnice nebo mimo.
Je-li N počet všech pokusů a T je počet těch, kterými jsme se trefili do čtvrtkruhu, spočítáme π jako:
π = 4T/N
Čím větší počet pokusů, tím víc se bude takto vypočítaná hodnota blížit π.
Proč to funguje?
Pravděpodobnost, že se trefíme do čtvrtkruhu, odpovídá povrchu čtvrtkruhu. Pravděpodobnost, že se trefíme do čtverce je 1 (generujeme pouze souřadnice uvnitř čtverce). Poměr plochy čtverec : čtvrtkruh je stejný jako poměr pravděpodobností zásah čtverce : zásah čtvrtkruhu. Poměr počtu pokusů N:T by měl při velkém počtu pokusů vycházet stejně. Plocha čtvrtkruhu při r=1 je rovna π/4. Jednoduchým výpočtem zjistíme, že vzoreček π = 4T/N skutečně platí.
Hledání nejkratších cest
Dále jsme ze zabývali Dijkstrovým algoritmem na hledání nejkratších cest, který jsme vyzkoušeli na následujícím grafu:
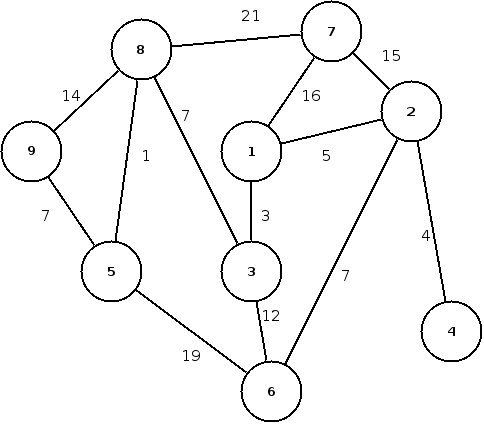
Dijkstrův algoritmus
dijkstra(s,G) { s - vychozi vrchol, G - reprezentace grafu }
{ stavy vrcholu: 'N'eviden, 'O'tevren, 'Z'avren }
stav: array[1..n] of char;
{ vzdalenost jednotlivych vrcholu od s }
dist: array[1..n] of integer;
{ predchudce vrcholu na nejkratsi ceste }
pred: array[1..n] of integer;
H: datova struktura s operacemi removeMin, insert a decrease;
{ inicializace }
stav .. stav[s]:= 'O', ostatni vrcholy 'N';
dist .. dist[s]:= 0, ostatni vrcholy +nekonecno;
pred .. inicializujeme treba -1;
H .. for all v: insert(v,H); { porovnavame podle dist[v] }
{ hlavni cyklus algoritmu }
1 while (existuje otevreny vrchol) do
2 v := removeMin(H);
3 stav[v]:= 'Z';
4 for all w: (w je soused v) do
5 if dist[w] > dist[v] + delta(v,w) then
6 D:= dist[w] - (dist[v] + delta(v,w));
7 decrease(w,D); { relaxujeme }
8 stav[w]:= 'O'; { otevreme vrchol }
9 pred[w]:= v; { predchudce w na nejkratsi ceste }
{ vysledek }
Delky nejkratsich cest jsou v poli dist
Nejkratsi cesta pro kazdy vrchol jde precist z pole pred
Do grafu G přistupujeme pokaždé, když zjišťujeme delta(v,w)(řádky 5 a 6),
nebo když potřebujeme zjistit sousedy vrcholu v (řádek 4).
Předpokládáme, že v grafu se nevyskytují záporné cykly a je souvislý.
Pokud jako strukturu H použijeme pole, bude mít algoritmus složitost
O(n^2) kde n je počet vrcholů. Pokud použijeme jako H binární haldu,
bude složitost o něco lepší - O(m*log(n)), kde m je počet hran (vyplývá to ze složitosti operace decrease a toho, že každý vrchol zavíráme právě jednou).
Třídící algoritmy
Na závěr jsme sestavili jakýsi seznam třídících algoritmů:
- bubble sort
- shake sort
- insert sort
- heap sort
- merge sort
- quick sort
- bogo sort
- radix sort
Všechny jsou vnitřní, což znamená, že pracují pouze v RAM. Oproti tomu vnější třídící algoritmy mohou ukládat mezivýsledky na HDD.
Pouze radix sort umí setřídit libovolnou vstupní permutaci prvků v lineárním čase, protože prvky neporovnává. Algoritmy, založené na porovnávání prvků mohou setřídit náhodnou permutaci n prvků nejlépe v čase n*log(n). Existuje na to důkaz, který bude/byl na přednášce. Pokud bude zájem, můžeme ho zopakovat i na cvičení.
Domácí úkol
Ověřte si, že jste členy skupiny M61LS. Od příštího cvičení už budou i nějaké příklady.
