Grafy
V úvodu cvičení jsme si zopakovali základní možnosti reprezentace grafů. Konkrétně jsme si na příkladech ukázali reprezentace pomocí:
- 1. matice sousednosti
- 2. matice incidence
- 3. seznamu následníků
- 4. seznamu hran
První tři způsoby jsou pěkně popsány zde spolu s dalšími užitečnými informacemi ke grafům.
Pro různé aplikace se hodí různé reprezentace. Každá reprezentace má své výhody i nevýhody. Matice incidence se například hodí pro reprezentaci řídkých grafů (málo hran). Z reprezentace pomocí seznamu následníků se zase dobře zjišťuje stupeň vrcholu.
Hledání nejkratších cest
Ve zbytku cvičení jsme ze zabývali Dijkstrovým algoritmem na hledání nejkratších cest, který jsme vyzkoušeli na následujícím grafu:
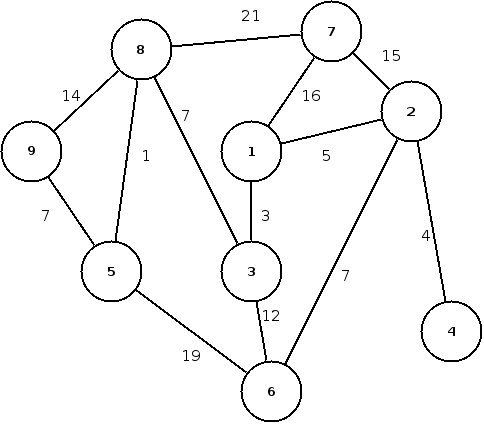
Dijkstrův algoritmus
dijkstra(s,G) { s - vychozi vrchol, G - reprezentace grafu }
{ stavy vrcholu: 'N'eviden, 'O'tevren, 'Z'avren }
stav: array[1..n] of char;
{ vzdalenost jednotlivych vrcholu od s }
dist: array[1..n] of integer;
{ predchudce vrcholu na nejkratsi ceste }
pred: array[1..n] of integer;
H: datova struktura s operacemi removeMin, insert a decrease;
{ inicializace }
stav .. stav[s]:= 'O', ostatni vrcholy 'N';
dist .. dist[s]:= 0, ostatni vrcholy +nekonecno;
pred .. inicializujeme treba -1;
H .. for all v: insert(v,H); { porovnavame podle dist[v] }
{ hlavni cyklus algoritmu }
1 while (existuje otevreny vrchol) do
2 v := removeMin(H);
3 stav[v]:= 'Z';
4 for all w: (w je soused v) do
5 if dist[w] > dist[v] + delta(v,w) then
6 D:= dist[w] - (dist[v] + delta(v,w));
7 decrease(w,D); { relaxujeme }
8 stav[w]:= 'O'; { otevreme vrchol }
9 pred[w]:= v; { predchudce w na nejkratsi ceste }
{ vysledek }
Delky nejkratsich cest jsou v poli dist
Nejkratsi cesta pro kazdy vrchol jde precist z pole pred
Do grafu G přistupujeme pokaždé, když zjišťujeme delta(v,w)(řádky 5 a 6),
nebo když potřebujeme zjistit sousedy vrcholu v (řádek 4).
Předpokládáme, že v grafu se nevyskytují záporné cykly a je souvislý.
Pokud jako strukturu H použijeme pole, bude mít algoritmus složitost
O(n^2) kde n je počet vrcholů. Pokud použijeme jako H binární haldu,
bude složitost o něco lepší - O(m*log(n)), kde m je počet hran (vyplývá to ze složitosti operace decrease a toho, že každý vrchol zavíráme právě jednou).
