Tables are presented in PDT row by row.

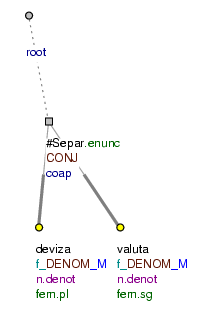
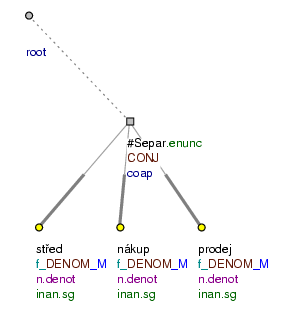
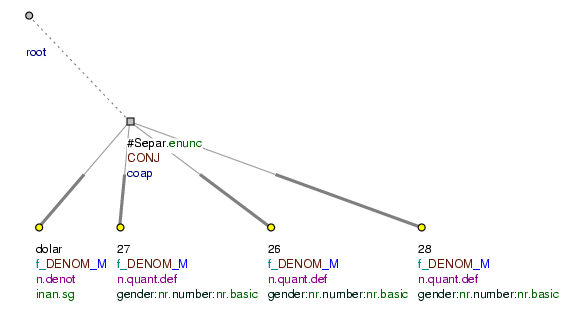
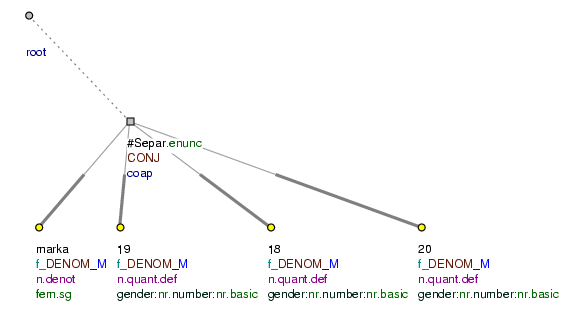
Tables whose meaning is difficult to interpret. In many tables, the meaning is difficult to interpret within the framework of individual rows, firstly because the meaning of the table is to be interpreted column by column and not only row by row, and secondly because the individual constructions do not possess morphology, but consist of nominative keywords. The annotation therefore represents individual items in the table only as co-ordinated nominative clauses (the effective roots are assigned the functor DENOM). The root of a paratactic structure is as a rule a newly established node with the t-lemma #Separ (as in the construction there is usually no punctuation). If individual items in the table have modifiers, the common rules for the analysis of components on a tectogrammatical level are followed.

Example of a table and model trees:

Cf. Fig. 8.231.

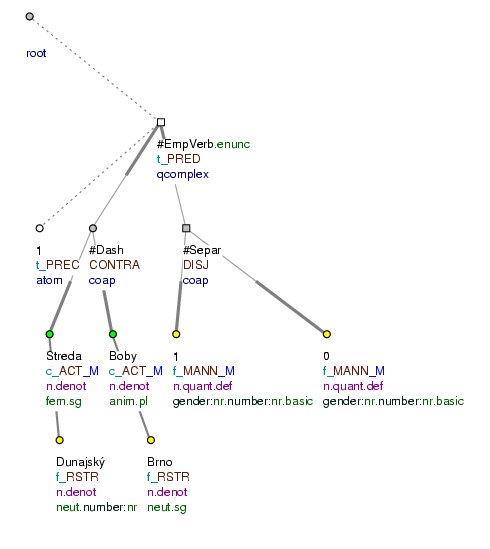
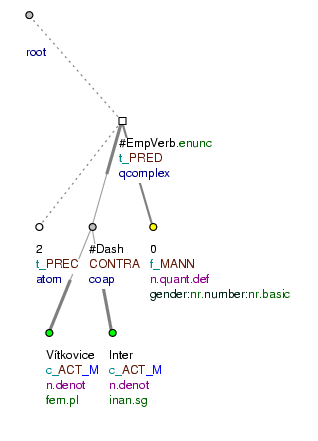
Interpretation of the meaning of the table is possible. However, if the meaning can be interpreted within the framework of individual rows (a row in the table carries meaning in itself, a verb can be posited in the construction and a morphology can be assigned to the construction), then a new node is inserted into the tectogrammatical tree for the empty verb (t_lemma=#EmpVerb; functor=PRED). Individual nodes are dependent on this newly established node and functors are assigned according to their function and their dependency w.r.t. the newly established node for a verb.

Example of a table and model trees:

Cf. Fig. 8.232.